回溯法
背景
回溯法(backtrack)常用于遍历列表所有子集,是 DFS 深度搜索一种,一般用于全排列,穷尽所有可能,遍历的过程实际上是一个决策树的遍历过程。时间复杂度一般 O(N!),它不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
模板
result = []
func backtrack(选择列表,路径):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(选择列表,路径)
撤销选择
核心就是从选择列表里做一个选择,然后一直递归往下搜索答案,如果遇到路径不通,就返回来撤销这次选择。
示例
subsets
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
遍历过程
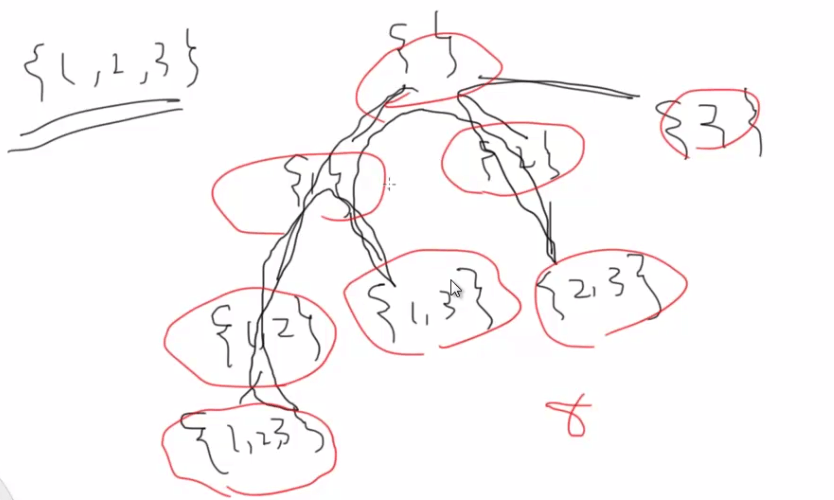
func subsets(nums []int) [][]int {
// 保存最终结果
result := make([][]int, 0)
// 保存中间结果
list := make([]int, 0)
backtrack(nums, 0, list, &result)
return result
}
// nums 给定的集合
// pos 下次添加到集合中的元素位置索引
// list 临时结果集合(每次需要复制保存)
// result 最终结果
func backtrack(nums []int, pos int, list []int, result *[][]int) {
// 把临时结果复制出来保存到最终结果
ans := make([]int, len(list))
copy(ans, list)
*result = append(*result, ans)
// 选择、处理结果、再撤销选择
for i := pos; i < len(nums); i++ {
list = append(list, nums[i])
backtrack(nums, i+1, list, result)
list = list[0 : len(list)-1]
}
}
subsets-ii
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。说明:解集不能包含重复的子集。
import (
"sort"
)
func subsetsWithDup(nums []int) [][]int {
// 保存最终结果
result := make([][]int, 0)
// 保存中间结果
list := make([]int, 0)
// 先排序
sort.Ints(nums)
backtrack(nums, 0, list, &result)
return result
}
// nums 给定的集合
// pos 下次添加到集合中的元素位置索引
// list 临时结果集合(每次需要复制保存)
// result 最终结果
func backtrack(nums []int, pos int, list []int, result *[][]int) {
// 把临时结果复制出来保存到最终结果
ans := make([]int, len(list))
copy(ans, list)
*result = append(*result, ans)
// 选择时需要剪枝、处理、撤销选择
for i := pos; i < len(nums); i++ {
// 排序之后,如果再遇到重复元素,则不选择此元素
if i != pos && nums[i] == nums[i-1] {
continue
}
list = append(list, nums[i])
backtrack(nums, i+1, list, result)
list = list[0 : len(list)-1]
}
}
permutations
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
思路:需要记录已经选择过的元素,满足条件的结果才进行返回
func permute(nums []int) [][]int {
result := make([][]int, 0)
list := make([]int, 0)
// 标记这个元素是否已经添加到结果集
visited := make([]bool, len(nums))
backtrack(nums, visited, list, &result)
return result
}
// nums 输入集合
// visited 当前递归标记过的元素
// list 临时结果集(路径)
// result 最终结果
func backtrack(nums []int, visited []bool, list []int, result *[][]int) {
// 返回条件:临时结果和输入集合长度一致 才是全排列
if len(list) == len(nums) {
ans := make([]int, len(list))
copy(ans, list)
*result = append(*result, ans)
return
}
for i := 0; i < len(nums); i++ {
// 已经添加过的元素,直接跳过
if visited[i] {
continue
}
// 添加元素
list = append(list, nums[i])
visited[i] = true
backtrack(nums, visited, list, result)
// 移除元素
visited[i] = false
list = list[0 : len(list)-1]
}
}
permutations-ii
给定一个可包含重复数字的序列,返回所有不重复的全排列。
import (
"sort"
)
func permuteUnique(nums []int) [][]int {
result := make([][]int, 0)
list := make([]int, 0)
// 标记这个元素是否已经添加到结果集
visited := make([]bool, len(nums))
sort.Ints(nums)
backtrack(nums, visited, list, &result)
return result
}
// nums 输入集合
// visited 当前递归标记过的元素
// list 临时结果集
// result 最终结果
func backtrack(nums []int, visited []bool, list []int, result *[][]int) {
// 临时结果和输入集合长度一致 才是全排列
if len(list) == len(nums) {
subResult := make([]int, len(list))
copy(subResult, list)
*result = append(*result, subResult)
}
for i := 0; i < len(nums); i++ {
// 已经添加过的元素,直接跳过
if visited[i] {
continue
}
// 上一个元素和当前相同,并且没有访问过就跳过
if i != 0 && nums[i] == nums[i-1] && !visited[i-1] {
continue
}
list = append(list, nums[i])
visited[i] = true
backtrack(nums, visited, list, result)
visited[i] = false
list = list[0 : len(list)-1]
}
}
练习
- [ ] subsets
- [ ] subsets-ii
- [ ] permutations
- [ ] permutations-ii
挑战题目