动态规划

背景

先从一道题目开始~

如题  triangle

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为  11（即，2 + 3 + 5 + 1 = 11）。

使用 DFS（遍历 或者 分治法）

遍历

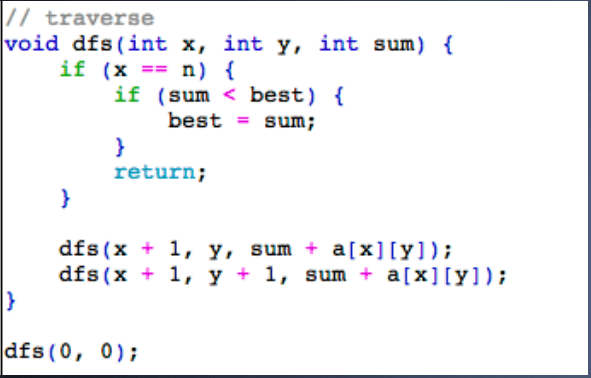
分治法

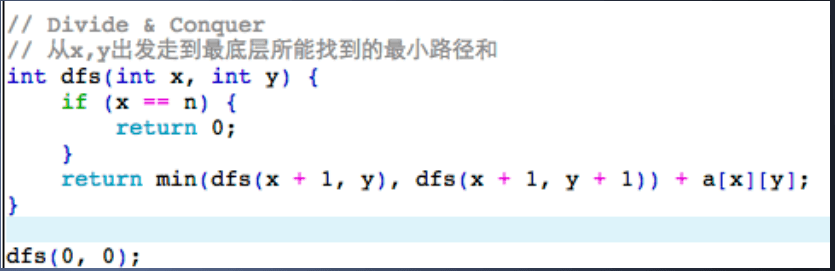
优化 DFS，缓存已经被计算的值（称为：记忆化搜索 本质上：动态规划）

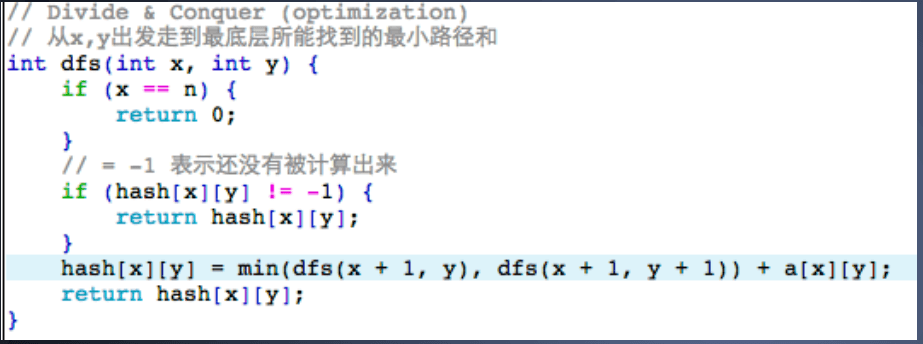
动态规划就是把大问题变成小问题，并解决了小问题重复计算的方法称为动态规划

动态规划和 DFS 区别

• 二叉树 子问题是没有交集，所以大部分二叉树都用递归或者分治法，即 DFS，就可以解决
• 像 triangle 这种是有重复走的情况，子问题是有交集，所以可以用动态规划来解决

动态规划，自底向上

func minimumTotal(triangle [][]int) int {
	if len(triangle) == 0 || len(triangle[0]) == 0 {
		return 0
	}
	// 1、状态定义：f[i][j] 表示从i,j出发，到达最后一层的最短路径
	var l = len(triangle)
	var f = make([][]int, l)
	// 2、初始化
	for i := 0; i < l; i++ {
		for j := 0; j < len(triangle[i]); j++ {
			if f[i] == nil {
				f[i] = make([]int, len(triangle[i]))
			}
			f[i][j] = triangle[i][j]
		}
	}
	// 3、递推求解
	for i := len(triangle) - 2; i >= 0; i-- {
		for j := 0; j < len(triangle[i]); j++ {
			f[i][j] = min(f[i+1][j], f[i+1][j+1]) + triangle[i][j]
		}
	}
	// 4、答案
	return f[0][0]
}
func min(a, b int) int {
	if a > b {
		return b
	}
	return a
}

动态规划，自顶向下

// 测试用例：
// [
// [2],
// [3,4],
// [6,5,7],
// [4,1,8,3]
// ]
func minimumTotal(triangle [][]int) int {
    if len(triangle) == 0 || len(triangle[0]) == 0 {
        return 0
    }
    // 1、状态定义：f[i][j] 表示从0,0出发，到达i,j的最短路径
    var l = len(triangle)
    var f = make([][]int, l)
    // 2、初始化
    for i := 0; i < l; i++ {
        for j := 0; j < len(triangle[i]); j++ {
            if f[i] == nil {
                f[i] = make([]int, len(triangle[i]))
            }
            f[i][j] = triangle[i][j]
        }
    }
    // 递推求解
    for i := 1; i < l; i++ {
        for j := 0; j < len(triangle[i]); j++ {
            // 这里分为两种情况：
            // 1、上一层没有左边值
            // 2、上一层没有右边值
            if j-1 < 0 {
                f[i][j] = f[i-1][j] + triangle[i][j]
            } else if j >= len(f[i-1]) {
                f[i][j] = f[i-1][j-1] + triangle[i][j]
            } else {
                f[i][j] = min(f[i-1][j], f[i-1][j-1]) + triangle[i][j]
            }
        }
    }
    result := f[l-1][0]
    for i := 1; i < len(f[l-1]); i++ {
        result = min(result, f[l-1][i])
    }
    return result
}
func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

递归和动规关系

递归是一种程序的实现方式：函数的自我调用

Function(x) {
	...
	Funciton(x-1);
	...
}

动态规划：是一种解决问 题的思想，大规模问题的结果，是由小规模问 题的结果运算得来的。动态规划可用递归来实现(Memorization Search)

使用场景

满足两个条件

• 满足以下条件之一
  • 求最大/最小值（Maximum/Minimum ）
  • 求是否可行（Yes/No ）
  • 求可行个数（Count(*) ）
• 满足不能排序或者交换（Can not sort / swap ）

如题：longest-consecutive-sequence  位置可以交换，所以不用动态规划

四点要素

1. 状态 State
   • 灵感，创造力，存储小规模问题的结果
2. 方程 Function
   • 状态之间的联系，怎么通过小的状态，来算大的状态
3. 初始化 Intialization
   • 最极限的小状态是什么, 起点
4. 答案 Answer
   • 最大的那个状态是什么，终点

常见四种类型

1. Matrix DP (10%)
2. Sequence (40%)
3. Two Sequences DP (40%)
4. Backpack (10%)

注意点

• 贪心算法大多题目靠背答案，所以如果能用动态规划就尽量用动规，不用贪心算法

1、矩阵类型（10%）

minimum-path-sum

给定一个包含非负整数的  m x n  网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

思路：动态规划 1、state: f[x][y]从起点走到 x,y 的最短路径 2、function: f[x][y] = min(f[x-1][y], f[x][y-1]) + A[x][y] 3、intialize: f[0][0] = A[0][0]、f[i][0] = sum(0,0 -> i,0)、 f[0][i] = sum(0,0 -> 0,i) 4、answer: f[n-1][m-1]

func minPathSum(grid [][]int) int {
    // 思路：动态规划
    // f[i][j] 表示i,j到0,0的和最小
    if len(grid) == 0 || len(grid[0]) == 0 {
        return 0
    }
    // 复用原来的矩阵列表
    // 初始化：f[i][0]、f[0][j]
    for i := 1; i < len(grid); i++ {
        grid[i][0] = grid[i][0] + grid[i-1][0]
    }
    for j := 1; j < len(grid[0]); j++ {
        grid[0][j] = grid[0][j] + grid[0][j-1]
    }
    for i := 1; i < len(grid); i++ {
        for j := 1; j < len(grid[i]); j++ {
            grid[i][j] = min(grid[i][j-1], grid[i-1][j]) + grid[i][j]
        }
    }
    return grid[len(grid)-1][len(grid[0])-1]
}
func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

unique-paths

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 问总共有多少条不同的路径？

func uniquePaths(m int, n int) int {
	// f[i][j] 表示i,j到0,0路径数
	f := make([][]int, m)
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if f[i] == nil {
				f[i] = make([]int, n)
			}
			f[i][j] = 1
		}
	}
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			f[i][j] = f[i-1][j] + f[i][j-1]
		}
	}
	return f[m-1][n-1]
}

unique-paths-ii

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 问总共有多少条不同的路径？ 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

func uniquePathsWithObstacles(obstacleGrid [][]int) int {
	// f[i][j] = f[i-1][j] + f[i][j-1] 并检查障碍物
	if obstacleGrid[0][0] == 1 {
		return 0
	}
	m := len(obstacleGrid)
	n := len(obstacleGrid[0])
	f := make([][]int, m)
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if f[i] == nil {
				f[i] = make([]int, n)
			}
			f[i][j] = 1
		}
	}
	for i := 1; i < m; i++ {
		if obstacleGrid[i][0] == 1 || f[i-1][0] == 0 {
			f[i][0] = 0
		}
	}
	for j := 1; j < n; j++ {
		if obstacleGrid[0][j] == 1 || f[0][j-1] == 0 {
			f[0][j] = 0
		}
	}
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			if obstacleGrid[i][j] == 1 {
				f[i][j] = 0
			} else {
				f[i][j] = f[i-1][j] + f[i][j-1]
			}
		}
	}
	return f[m-1][n-1]
}

2、序列类型（40%）

climbing-stairs

假设你正在爬楼梯。需要  n  阶你才能到达楼顶。

func climbStairs(n int) int {
    // f[i] = f[i-1] + f[i-2]
    if n == 1 || n == 0 {
        return n
    }
    f := make([]int, n+1)
    f[1] = 1
    f[2] = 2
    for i := 3; i <= n; i++ {
        f[i] = f[i-1] + f[i-2]
    }
    return f[n]
}

jump-game

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个位置。

func canJump(nums []int) bool {
    // 思路：看最后一跳
    // 状态：f[i] 表示是否能从0跳到i
    // 推导：f[i] = OR(f[j],j<i&&j能跳到i) 判断之前所有的点最后一跳是否能跳到当前点
    // 初始化：f[0] = 0
    // 结果： f[n-1]
    if len(nums) == 0 {
        return true
    }
    f := make([]bool, len(nums))
    f[0] = true
    for i := 1; i < len(nums); i++ {
        for j := 0; j < i; j++ {
            if f[j] == true && nums[j]+j >= i {
                f[i] = true
            }
        }
    }
    return f[len(nums)-1]
}

jump-game-ii

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 你的目标是使用最少的跳跃次数到达数组的最后一个位置。

// v1动态规划（其他语言超时参考v2）
func jump(nums []int) int {
    // 状态：f[i] 表示从起点到当前位置最小次数
    // 推导：f[i] = f[j],a[j]+j >=i,min(f[j]+1)
    // 初始化：f[0] = 0
    // 结果：f[n-1]
    f := make([]int, len(nums))
    f[0] = 0
    for i := 1; i < len(nums); i++ {
        // f[i] 最大值为i
        f[i] = i
        // 遍历之前结果取一个最小值+1
        for j := 0; j < i; j++ {
            if nums[j]+j >= i {
                f[i] = min(f[j]+1,f[i])
            }
        }
    }
    return f[len(nums)-1]
}
func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

// v2 动态规划+贪心优化
func jump(nums []int) int {
    n:=len(nums)
    f := make([]int, n)
    f[0] = 0
    for i := 1; i < n; i++ {
        // 取第一个能跳到当前位置的点即可
        // 因为跳跃次数的结果集是单调递增的，所以贪心思路是正确的
        idx:=0
        for idx<n&&idx+nums[idx]<i{
            idx++
        }
        f[i]=f[idx]+1
    }
    return f[n-1]
}

palindrome-partitioning-ii

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。 返回符合要求的最少分割次数。

func minCut(s string) int {
	// state: f[i] "前i"个字符组成的子字符串需要最少几次cut(个数-1为索引)
	// function: f[i] = MIN{f[j]+1}, j < i && [j+1 ~ i]这一段是一个回文串
	// intialize: f[i] = i - 1 (f[0] = -1)
	// answer: f[s.length()]
	if len(s) == 0 || len(s) == 1 {
		return 0
	}
	f := make([]int, len(s)+1)
	f[0] = -1
	f[1] = 0
	for i := 1; i <= len(s); i++ {
		f[i] = i - 1
		for j := 0; j < i; j++ {
			if isPalindrome(s, j, i-1) {
				f[i] = min(f[i], f[j]+1)
			}
		}
	}
	return f[len(s)]
}
func min(a, b int) int {
	if a > b {
		return b
	}
	return a
}
func isPalindrome(s string, i, j int) bool {
	for i < j {
		if s[i] != s[j] {
			return false
		}
		i++
		j--
	}
	return true
}

注意点

• 判断回文字符串时，可以提前用动态规划算好，减少时间复杂度

longest-increasing-subsequence

给定一个无序的整数数组，找到其中最长上升子序列的长度。

func lengthOfLIS(nums []int) int {
    // f[i] 表示从0开始到i结尾的最长序列长度
    // f[i] = max(f[j])+1 ,a[j]<a[i]
    // f[0...n-1] = 1
    // max(f[0]...f[n-1])
    if len(nums) == 0 || len(nums) == 1 {
        return len(nums)
    }
    f := make([]int, len(nums))
    f[0] = 1
    for i := 1; i < len(nums); i++ {
        f[i] = 1
        for j := 0; j < i; j++ {
            if nums[j] < nums[i] {
                f[i] = max(f[i], f[j]+1)
            }
        }
    }
    result := f[0]
    for i := 1; i < len(nums); i++ {
        result = max(result, f[i])
    }
    return result

}
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

word-break

给定一个非空字符串  s  和一个包含非空单词列表的字典  wordDict，判定  s  是否可以被空格拆分为一个或多个在字典中出现的单词。

func wordBreak(s string, wordDict []string) bool {
	// f[i] 表示前i个字符是否可以被切分
	// f[i] = f[j] && s[j+1~i] in wordDict
	// f[0] = true
	// return f[len]

	if len(s) == 0 {
		return true
	}
	f := make([]bool, len(s)+1)
	f[0] = true
	max,dict := maxLen(wordDict)
	for i := 1; i <= len(s); i++ {
		l := 0
		if i - max > 0 {
			l = i - max
		}
		for j := l; j < i; j++ {
			if f[j] && inDict(s[j:i],dict) {
				f[i] = true
                break
			}
		}
	}
	return f[len(s)]
}



func maxLen(wordDict []string) (int,map[string]bool) {
    dict := make(map[string]bool)
	max := 0
	for _, v := range wordDict {
		dict[v] = true
		if len(v) > max {
			max = len(v)
		}
	}
	return max,dict
}

func inDict(s string,dict map[string]bool) bool {
	_, ok := dict[s]
	return ok
}

小结

常见处理方式是给 0 位置占位，这样处理问题时一视同仁，初始化则在原来基础上 length+1，返回结果 f[n]

• 状态可以为前 i 个
• 初始化 length+1
• 取值 index=i-1
• 返回值：f[n]或者 f[m][n]

Two Sequences DP（40%）

longest-common-subsequence

给定两个字符串  text1 和  text2，返回这两个字符串的最长公共子序列。 一个字符串的   子序列   是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

func longestCommonSubsequence(a string, b string) int {
    // dp[i][j] a前i个和b前j个字符最长公共子序列
    // dp[m+1][n+1]
    //   ' a d c e
    // ' 0 0 0 0 0
    // a 0 1 1 1 1
    // c 0 1 1 2 1
    //
    dp:=make([][]int,len(a)+1)
    for i:=0;i<=len(a);i++ {
        dp[i]=make([]int,len(b)+1)
    }
    for i:=1;i<=len(a);i++ {
        for j:=1;j<=len(b);j++ {
            // 相等取左上元素+1，否则取左或上的较大值
            if a[i-1]==b[j-1] {
                dp[i][j]=dp[i-1][j-1]+1
            } else {
                dp[i][j]=max(dp[i-1][j],dp[i][j-1])
            }
        }
    }
    return dp[len(a)][len(b)]
}
func max(a,b int)int {
    if a>b{
        return a
    }
    return b
}

注意点

• go 切片初始化

dp:=make([][]int,len(a)+1)
for i:=0;i<=len(a);i++ {
    dp[i]=make([]int,len(b)+1)
}

• 从 1 开始遍历到最大长度
• 索引需要减一

edit-distance

给你两个单词  word1 和  word2，请你计算出将  word1  转换成  word2 所使用的最少操作数   你可以对一个单词进行如下三种操作： 插入一个字符 删除一个字符 替换一个字符

思路：和上题很类似，相等则不需要操作，否则取删除、插入、替换最小操作次数的值+1

func minDistance(word1 string, word2 string) int {
    // dp[i][j] 表示a字符串的前i个字符编辑为b字符串的前j个字符最少需要多少次操作
    // dp[i][j] = OR(dp[i-1][j-1]，a[i]==b[j],min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1)
    dp:=make([][]int,len(word1)+1)
    for i:=0;i<len(dp);i++{
        dp[i]=make([]int,len(word2)+1)
    }
    for i:=0;i<len(dp);i++{
        dp[i][0]=i
    }
    for j:=0;j<len(dp[0]);j++{
        dp[0][j]=j
    }
    for i:=1;i<=len(word1);i++{
        for j:=1;j<=len(word2);j++{
            // 相等则不需要操作
            if word1[i-1]==word2[j-1] {
                dp[i][j]=dp[i-1][j-1]
            }else{ // 否则取删除、插入、替换最小操作次数的值+1
                dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1
            }
        }
    }
    return dp[len(word1)][len(word2)]
}
func min(a,b int)int{
    if a>b{
        return b
    }
    return a
}

说明

另外一种做法：MAXLEN(a,b)-LCS(a,b)

零钱和背包（10%）

coin-change

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回  -1。

思路：和其他 DP 不太一样，i 表示钱或者容量

func coinChange(coins []int, amount int) int {
    // 状态 dp[i]表示金额为i时，组成的最小硬币个数
    // 推导 dp[i]  = min(dp[i-1], dp[i-2], dp[i-5])+1, 前提 i-coins[j] > 0
    // 初始化为最大值 dp[i]=amount+1
    // 返回值 dp[n] or dp[n]>amount =>-1
    dp:=make([]int,amount+1)
    for i:=0;i<=amount;i++{
        dp[i]=amount+1
    }
    dp[0]=0
    for i:=1;i<=amount;i++{
        for j:=0;j<len(coins);j++{
            if  i-coins[j]>=0  {
                dp[i]=min(dp[i],dp[i-coins[j]]+1)
            }
        }
    }
    if dp[amount] > amount {
        return -1
    }
    return dp[amount]

}
func min(a,b int)int{
    if a>b{
        return b
    }
    return a
}

注意

dp[i-a[j]] 决策 a[j]是否参与

backpack

在 n 个物品中挑选若干物品装入背包，最多能装多满？假设背包的大小为 m，每个物品的大小为 A[i]

func backPack (m int, A []int) int {
    // write your code here
    // f[i][j] 前i个物品，是否能装j
    // f[i][j] =f[i-1][j] f[i-1][j-a[i] j>a[i]
    // f[0][0]=true f[...][0]=true
    // f[n][X]
    f:=make([][]bool,len(A)+1)
    for i:=0;i<=len(A);i++{
        f[i]=make([]bool,m+1)
    }
    f[0][0]=true
    for i:=1;i<=len(A);i++{
        for j:=0;j<=m;j++{
            f[i][j]=f[i-1][j]
            if j-A[i-1]>=0 && f[i-1][j-A[i-1]]{
                f[i][j]=true
            }
        }
    }
    for i:=m;i>=0;i--{
        if f[len(A)][i] {
            return i
        }
    }
    return 0
}

backpack-ii

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值. 问最多能装入背包的总价值是多大?

思路：f[i][j] 前 i 个物品，装入 j 背包 最大价值

func backPackII (m int, A []int, V []int) int {
    // write your code here
    // f[i][j] 前i个物品，装入j背包 最大价值
    // f[i][j] =max(f[i-1][j] ,f[i-1][j-A[i]]+V[i]) 是否加入A[i]物品
    // f[0][0]=0 f[0][...]=0 f[...][0]=0
    f:=make([][]int,len(A)+1)
    for i:=0;i<len(A)+1;i++{
        f[i]=make([]int,m+1)
    }
    for i:=1;i<=len(A);i++{
        for j:=0;j<=m;j++{
            f[i][j]=f[i-1][j]
            if j-A[i-1] >= 0{
                f[i][j]=max(f[i-1][j],f[i-1][j-A[i-1]]+V[i-1])
            }
        }
    }
    return f[len(A)][m]
}
func max(a,b int)int{
    if a>b{
        return a
    }
    return b
}

练习

Matrix DP (10%)

• [ ] triangle
• [ ] minimum-path-sum
• [ ] unique-paths
• [ ] unique-paths-ii

Sequence (40%)

• [ ] climbing-stairs
• [ ] jump-game
• [ ] jump-game-ii
• [ ] palindrome-partitioning-ii
• [ ] longest-increasing-subsequence
• [ ] word-break

Two Sequences DP (40%)

• [ ] longest-common-subsequence
• [ ] edit-distance

Backpack & Coin Change (10%)

• [ ] coin-change
• [ ] backpack
• [ ] backpack-ii